the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Airborne polarimetric Doppler weather radar: trade-offs between various engineering specifications
Eric Loew
NCAR EOL is investigating potential configurations for the next-generation airborne phased array radar (APAR) that is capable of retrieving dynamic and microphysical characteristics of clouds and precipitation. The APAR will operate at C band. The APAR will use the electronic scanning (e-scan) feature to acquire the optimal number of independent samples for recording research-quality measurements. Since the airborne radar has only a limited time for collecting measurements over a specified region (moving aircraft platform ∼ 100 m s−1), beam multiplexing will significantly enhance its ability to collect high-resolution, research-quality measurements. Beam multiplexing reduces errors in radar measurements while providing rapid updates of scan volumes. Beamwidth depends on the size of the antenna aperture. Beamwidth and directivity of elliptical, circular, and rectangular antenna apertures are compared and radar sensitivity is evaluated for various polarimetric configurations and transmit–receive (T/R) elements. In the case of polarimetric measurements, alternate transmit with alternate receive (single-channel receiver) and simultaneous reception (dual-channel receiver) is compared. From an overall architecture perspective, element-level digitization of T/R module versus digital sub-array is considered with regard to flexibility in adaptive beamforming, polarimetric performance, calibration, and data quality. Methodologies for calibration of the radar and removing bias in polarimetric measurements are outlined. The above-mentioned engineering options are evaluated for realizing an optimal APAR system suitable for measuring the high temporal and spatial resolutions of Doppler and polarimetric measurements of precipitation and clouds.
Characterizing location, intensity, and motion of hurricanes, tornados, and extreme precipitation events and understanding effects of clouds and aerosols on the earth radiation budget requires a better understanding of the kinematic (storm motion and structure) and microphysical processes (particle growth, phase changes) within these storms. This remains a challenge for both the scientific and operational communities. Observing these events is challenging using ground-based radars as the conditions that lead to high-impact events typically occur in remote areas (e.g., hurricanes over the ocean, orographic precipitation in rugged terrain) or because of large uncertainties on the timing and location (e.g., tornado, extreme precipitation events) related to suboptimal radar coverage. Airborne radar is a powerful tool to observe weather systems, in particular, storms over complex terrain, the ocean, polar regions, and forest regions not easily observable by ground-based radars (Bluestein and Wakimoto, 2003). A scanning Doppler radar on an airborne platform is used for estimating dual-Doppler winds with the help of rapid scanning as the aircraft flies past a storm (Hildebrand et al., 1996). Scanning Doppler radar with dual-polarization capability on an airborne platform is capable of measuring dual-Doppler winds and retrieving particle types (ice or water) and shapes and liquid–ice water contents using reflectivity (Z), differential reflectivity (ZDR), specific propagation phase (KDP), and linear depolarization ratio (LDR).
At present, no other instrument other than an airborne polarimetric Doppler phased array radar (APAR) system has the potential to estimate high temporal and spatial measurements of 3-D winds and microphysics concurrently (Vivekanandan et al., 2014). NCAR's Earth Observing Laboratory (EOL) is currently conducting a design study for a future APAR.
Between 1992 and 2013 NCAR operated the research-quality Doppler radar, ELDORA/ASTRAIA (Electra Doppler Radar/Analyese Steroscopic par Impulsions Aeroporte, hereafter referred as ELDORA). The ELDORA was configured with dual-slotted waveguide array antennas using a dual-transmitter, dual-beam, rapid-scan, and step-chirped waveform (Girardin-Gondeau et al., 1991) that significantly improved the along-track spatial resolution from 750 to 300 m when compared to NOAA's airborne tail Doppler radar (TDR) (Hildebrand et al., 1996). The ELDORA was jointly developed by NCAR and the Centre d'Étude des Environments Terrestre et Planétaires (CETP), France. In recent years, CETP became LATMOS (Laboratoire Atmospheres, Milieux, Observations Spatiales). It collects research-quality Doppler and reflectivity measurements that continue to set the standard for airborne radar; however, ELDORA X-band radar's penetration into precipitation is limited by attenuation and it is not designed to collect polarimetric measurements to remotely estimate microphysics. ELDORA has been placed in dormancy because its airborne platform (Naval Research Lab P-3 587) was retired in January 2013. The US research community has strongly voiced the need to continue measurement capability similar to that provided by ELDORA (Smith et al., 2012).
The combination of remote and in situ sensors on a single airborne platform will serve the observational needs for broader scientific communities of cloud microphysics, mesoscale meteorology, atmospheric chemistry, and climate, and it will fill a critical gap in the current airborne observing facilities. An APAR deployed on aircraft with long on-station time, such as the C-130, will allow investigation of weather systems such as monsoons, tropical cyclones, severe convection over continents, orographic precipitation, convection over the oceans, and polar and low to middle atmospheric chemistry. A schematic of the APAR antenna panels on the C-130 is shown in Fig. 1. APAR will feature four removable C-band active electronically scanned arrays (AESAs) mounted on top, both sides, and the bottom of the aircraft. Each antenna will have dual-Doppler and polarimetric capabilities. This configuration, when integrated with data from the NSF/NCAR C-130 nose radar, will provide 360∘ horizontal surveillance radar scan coverage and volumetric data collection. Radar products can be displayed in real time. The AESA placement provides for flexible scanning capabilities for 3-D data volume generation.
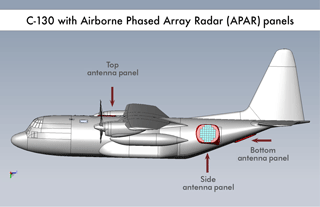
Figure 1Notional schematic of APAR's four AESA antenna panel placements on the C-130. There are two side panels on port and starboard of the fuselage, third panel on the top, and the fourth panel at the rear ramp.
The real-time radar displays on the aircraft provide situational awareness to aircraft pilots allowing for safe aircraft operations in the vicinity of extreme weather. The 3-D volume-scan data not only can help guide the NSF/NCAR C-130 research in and around weather of interest but also has the potential to be used to guide other aircraft conducting research in the vicinity. The C-130 is a versatile and capable research platform that carries a wide variety of scientific payloads. The C-130 has a 10 h flight endurance, a 5400 km range at up to 8.2 km altitude, and a payload capacity of up to 5900 kg. NCAR EOL/RAF maintains the NSF/NCAR C-130 aircraft in its fleet for airborne atmospheric measurements, including dropsonde, in situ sampling, and remote sensing of clouds, chemistry, and aerosols.
This paper is organized as follows. Section 2 describes radar system and its major subsystems. Rationale for selection of transmit frequency is presented in Sect. 3. Discussions related to polarimetric configurations and advantage of agile beam scanning are presented in Sects. 4 and 5. Various antenna aperture configurations and corresponding beamwidth characteristics are presented in Sect. 6. The sensitivity of the radar measurements depends on transmit and receive hardware characteristics, polarimetric measurement configuration, and signal processing. Expected radar sensitivity as a function of a few key parameters is discussed in Sect. 7. PAR with digital architecture is amenable for consistently maintaining data quality, deployment of radar with repeatable and robust calibration, and formation of fan-beam and pencil-beam configuration for imaging rapidly changing weather system. In this regard possible analog and digital beamforming architecture configurations are compared in Sect. 8. A brief description of calibration requirement is discussed in Sect. 9. Estimates of biases in radar measurements as a result of cross coupling in polarimetric mode is shown in Sect. 10. Section 11 presents a summary.
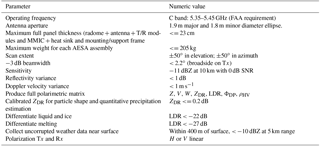
Preliminary design specifications of peak power, beamwidth, dual-polarimetric configuration, scan timing sequences, and signal processing are outlined in Vivekanandan et al. (2014); some key technical specifications are presented in Table 1. The APAR will operate at C band. It will use the e-scan feature to acquire the optimal number of independent samples for achieving 1 m s−1 accuracy in radial velocity, 1 dB in Z, and 0.2 dB in ZDR accuracies with a sensitivity of −11 dBZ at 10 km. Since the airborne radar has only a limited time for collecting measurements over a specified region (moving aircraft platform ∼ 100 m s−1), beam multiplexing will significantly enhance its ability to collect high-resolution, research-quality measurements. Beam multiplexing reduces errors in radar measurements while providing rapid updates of scan volumes (Weber et al., 2007; Yu et al., 2007).

Figure 2Simplified block diagram of PAR. It consists of six components: (1) array antenna front end, (2) T/R modules, (3) array antenna backplane, (4) radar back end, (5) radar processor and display, and (6) radar scheduler.
From an overall architecture perspective, element-level digitization of transmit–receive (T/R) module versus digital sub-array has to be carefully considered with regard to flexibility in adaptive beamforming, polarimetric performance, calibration, and imaging of rapidly moving weather systems. For achieving desired sensitivity and range resolution, pulse compression is proposed, with a compression gain of at least 15 dB. However, this will require transmission of short pulses for covering the blind zone created by the strong pulse at the expense of overall radar sensitivity due to long and short pulses. A staggered pulse repetition frequency (PRF) technique for extending Doppler Nyquist interval was extremely valuable for the ELDORA is considered, but its evaluation is beyond the scope of this document.
It is common for phased array radar (PAR) antennas to be modular in design. Figure 2 shows a conceptual block diagram of the radar system. The radar block diagram is divided into two main parts: the front end and the back end. The front end consists of all parts of the phased array which reside outside the fuselage of the aircraft and is represented by three items: (i) the radio frequency (RF) array antenna front end, (ii) T/R modules, and (iii) array antenna backplane in Fig. 2. The RF array antenna front end includes low-profile dual-polarization antenna element radiators, a power distribution board, and a data distribution board. Each radiating element will use a stacked patched microstrip antenna radiator coupled to a T/R module. The microstrip patch antenna elements can transmit in either horizontal (H) or vertical (V) polarizations. The radiating elements are spaced less than half a wavelength apart to avoid grating lobes over the full scan extent (Wang et al., 2008). The proposed dual-polarized patch antenna element overcomes the problems of isolation in the diagonal plane and mismatch between the horizontal and vertical co-polarizations by combining the features of a parasitic crosspatch antenna and a ground plane with a cross-shaped aperture and capacitive and inductive loading corners. The patch is fed symmetrically in both horizontal and vertical polarizations. The radar back end consists of all parts of the system that reside inside the aircraft cabin and is represented by the (i) radar digital back end, (ii) radar processor/display, and (iii) radar scheduler in Fig. 2.
The desired goal is to meet or exceed the current sensitivity and spatial resolution of the ELDORA radar while adding polarimetric capability. The ELDORA is a four-frequency system and hence produces nearly four times the number of independent samples as a conventional, single-frequency radar. To match the reflectivity and velocity variances achieved by ELDORA in the same time interval, the pulse compression is used. This requires that APAR bandwidth (Tx and Rx) be increased by a factor of 4 and four range gates averaged. Also, to match the sensitivity of a high-peak-power radar, it is generally recognized that to accomplish this with solid-state power amplifiers (PAs), the use of pulse compression is essential. When using pulse compression in order to recover the close-in range obscured by the longer, compressed pulse, short, single-frequency pulse(s) must also be used. For APAR two such “filler” pulses at different frequencies must be transmitted each pulse repetition time. This is necessary to have sufficient independent samples to reduce reflectivity and velocity variances while still achieving the desired along-track resolution.
The T/R module consists of a matrix of individual T/R modules. It is a multi-layer printed circuit board that includes monolithic microwave integrated circuit (MMIC) components, namely, digital phase shifters, attenuators, a PA, low noise amplifier (LNA), various drive amplifiers, high-speed field effect transistor switches, and a field programmable gate array (FPGA). The digital 6-bit phase shifter supplies the necessary phase to the RF signal for steering the beam in a specified direction. The digital attenuator tapers transmit and receive amplitudes across the active aperture for reducing antenna sidelobes and also for aligning the amplitudes of each T/R element. Transmit and receive amplitudes are tapered across the aperture to lower sidelobes. Various aperture-tapering options are presented in Sect. 7.
The high-power amplifier (HPA) amplifies the RF transmit signal and is capable of handling short and long pulses. It dissipates a significant amount of power and the heat generated must be removed for safe operation of the T/R module. The HPA has the shortest lifetime among all of the components in the T/R module due to its self-heating. Heat sinks are placed outward into the space between the antenna aperture and backplane printed circuit boards. Cooling can be accomplished via forced air convection or a liquid cooling via a cold plate. The LNA determines the noise figure of the receive chain and it is placed closest to the receive port of the antenna. Each T/R element is coupled to a two-port radiator for dual-polarization transmission and reception. An FPGA controls the attenuator, phase shifter, and switches for the desired performance of APAR.
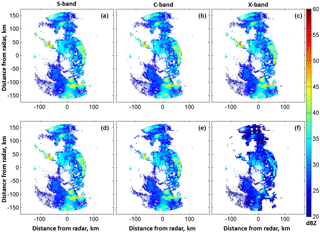
Figure 3Panels (a, b, c) indicate the reflectivity without attenuation simulated from DSD for S-, C-, and X-band polarimetric radar, respectively, on 17 September 1998, 22:11 UTC. Panels (d, e, f) indicate the measured reflectivity with attenuation effect for S-, C-, and X-band polarimetric radar, respectively. The radar is located in the center of each panel.
The radar back end includes master FPGAs for communicating scan angle, polarization, and pulse information to the FPGAs in each line replaceable unit from the radar scheduler. The radar back end consists of up and down converters between intermediate frequency and RF, digital transceivers, and a host computer for generating radar measurements including mean velocity, spectrum width, and dual-polarimetric observables and associated displays for all generated parameters.
X-band and shorter wavelengths are preferred choices for mobile ground-based and airborne deployments because the radar antenna is much smaller in size than the S-band or C-band antennas for a specified beam width. The larger backscatter cross section of particle sizes smaller than the wavelength (Rayleigh scattering) significantly improves the detection limit (Lhermitte, 1987; Clothiaux et al., 1995). In the Rayleigh scattering regime, the radar cross section at X band is 10 and 20 dB larger than at C band and S band, respectively. For a specified transmit power and antenna gain, X-band radar is also more sensitive to detecting lighter precipitation than S- or C-band radar. However, a major disadvantage of the X-band radar signal is that it is more susceptible to attenuation than an S-band and C-band radar signal. The intervening precipitation between radar and measurement volume causes attenuation. The amount of attenuation is proportional to the intensity of precipitation. Horizontal X-band co-polarization reflectivity (ZHH) and ZDR are usually underestimated due to attenuation of the radar signal as it propagates through precipitation. Attenuation in precipitation at X band is about a factor of 5 to 7 times larger when compared to C band (Bringi and Chandrasekar, 2001). In the case of rain, KDP is proportional to rain intensity. Attenuation and specific differential attenuation are almost linearly proportional to KDP (Bringi et al., 1990). As KDP is unaffected by attenuation radar system bias due to change in transmit power and antenna and receiver gain factors, it is more commonly used for attenuation correction.
In order to characterize the effect of attenuation on S-, C-, and X-band polarimetric radar measurements, intrinsic ZHH and attenuated ZHH were simulated for a rain event. The rain medium is characterized by a drop size distribution (DSD). Polarimetric radar measurements at S band are used for estimating DSD (Brandes et al., 2004). The data used in this study were collected in east-central Florida during the summer of 1998 in a special experiment. For the retrieved DSDs, ZHH and attenuated ZHH in S-, C-, and X-band polarimetric were simulated using rigorous electromagnetic scattering cross sections (Vivekanandan et al., 2004).
Intrinsic reflectivities without considering the attenuation effect were almost similar in S, C, and X as shown in Fig. 3a, b, and c except there are subtle differences due to Mie scattering at C and X bands. However, effects of attenuation on reflectivity are noticeable in Fig. 3e and f. In the regions south of the radar, X-band reflectivity is severely attenuated and the precipitation is not detected. In comparison with X band, the C-band reflectivity is weakly attenuated. In this example, the convection system produced about 0.04, 0.4, and 2 dB km−1 of attenuation at S, C, and X bands, respectively. The maximum total accumulated attenuation could reach about 1.2, 10, and 30 dB for S, C, and X band, respectively. X-band radar is subjected to the most significant attenuation in precipitation systems and the S-band radar has the least attenuation. The C-band radar signals experience less attenuation when compared to X-band radar signals.
However, attenuated C-band radar measurements must be corrected for attenuation effects before retrieving rain rate and microphysical information from them. The attenuation correction based on the AH–ZHH empirical relation is also unstable and sensitive to the calibration error in ZHH. The accuracy and stability of the attenuation correction scheme is vastly improved when dual-polarimetric observations are used (Bringi et al., 1990). Considering limited antenna aperture area on C-130 fuselage, deeper penetration of C-band signals into squall lines and rainbands due to lower attenuation at C band than at X band, and the availability of more stable and accurate attenuation correction scheme using polarimetric radar measurements, C band was selected as the operating wavelength for the APAR.
Weather radars make polarimetric measurements in two distinct T/R modes: (i) alternate transmit and simultaneously receive (ATSR) and (ii) simultaneously transmit and simultaneously receive (STSR). Any cross coupling between horizontally (H) and vertically (V) transmitted or received waves in the hardware and/or propagation medium due to canted hydrometeors would bias ZDR measurement. Cross-polarization isolation requirement is less stringent for estimating unbiased ZHH and ZDR in the ATSR mode than in the STSR mode. Cross-polarization isolation depends on the integrated cross-polar ratio (ICPR) of the radiating elements, cross-polar system phase (phase difference between co- and cross channels), and the ΦDP of the precipitation medium in the STSR mode. Assuming the system phase characteristic is known, ICPR < −23 dB is required for estimating ZDR with less than 0.2 dB bias (Wang and Chandrasekar, 2006). In ATSR mode ICPR < −20 dB is satisfactory for estimating ZDR with less than 0.2 dB bias. Also, in the STSR mode, cross-polarization measurement is not feasible as radar transmits in both horizontal and vertical polarizations simultaneously. However, for ICPR, better than −33 dB is required for measuring intrinsic LDR of −27 dB (Bringi and Chandrasekar, 2001). As the most desired measurement in a polarization configuration is ZDR, the alternate transmit mode is a preferred one for the proposed APAR.
APAR system can be designed to operate in one of two alternating transmit modes:
-
ATSR, which requires two receive channels;
-
ATAR (alternate transmit and alternate receive), which requires one receive channel.
In the alternating transmit mode, both cross- and co-polar measurements, i.e., full scattering matrix, are available. The ATSR mode requires twice the amount of time as the STSR mode for acquiring measurements as it alternates between H and V transmit polarizations.
The primary polarimetric capability is to compute co-polar parameters, e.g., ZDR, KDP, and co-polar correlation coefficient (ρHV). To achieve this objective, horizontal and vertical antenna patterns (main beam) must be in excellent agreement spatially. This applies to both to the broadside and as the beam is scanned in azimuth and elevation. A secondary polarimetric capability is to produce quality cross-polar measurements, like LDR. Two factors govern the ability to make accurate cross-polar measurements. First, there needs to be sufficient signal in the co-polar channel; signal-to-noise ratio (SNR) in the co-polar channel must be greater than or equal to the LDR or the hydrometeors. Second, isolation between the co-polar and cross-polar channels must be at least 6 dB greater than the desired LDR lower limit. In practice this isolation is relatively easy to achieve in the T/R module and downstream radar hardware. So, antenna performance is usually the limiting factor. The antenna's (two-way) ICPR is the defining property. ICPR is defined as
where fhh and fvv are the co-polar antenna patterns (amplitude and phase), and fvh and fhv are the cross-polar antenna patterns (amplitude and phase). The first index in the subscript denotes the transmit polarization, while the second index denotes the receive polarization. φ is azimuth angle in radians and θ is the elevation angle in radians.
As mentioned earlier, for estimating intrinsic LDR of −27 dB within 1 dB error, T/R isolation, i.e., ICPR, must be < −33 dB (Bringi and Chandrasekar, 2001). This applies not only to broadside but also as the beam is scanned in azimuth and elevation. In the case of an electronically scanned aperture array (ESA), when a beam is steered electronically away from the boresight, the transmitted field is biased as a function of scan angle and cross coupling between dual-polarization sources occur (Zhang, 2017). In order to limit the effect of differential gain and beam pattern on polarimetric measurements, co-polarization measurements will be collected only up to 20∘ from broadside. A detailed discussion regarding gain changes and cross coupling is presented in Sect. 10.
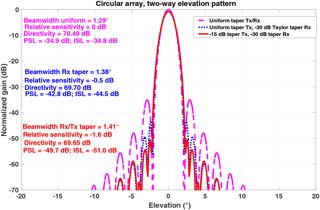
Figure 7Transmit and receive patterns of the circular aperture for three different tapering: (i) uniform tapering for both transmit and receive, (ii) uniform transmit and 30 dB Taylor taper for the receive, and (iii) 15 and 30 dB Taylor tapering of transmit and receive aperture.
Another key aspect of PARs is the ability to form multiple, simultaneous beams upon reception using digital beamforming techniques. Although this capability would not routinely be part of the APAR mission, in certain high-impact weather cases it would be extremely useful. Specifically, it would be desirable to have the ability to spoil the transmit beam to allow for a 20∘ fan beam in elevation, steerable in azimuth, and receive a separate RF signal(s) for each row of the array. A brief description of various PAR architectures with regard to digital and analog beamforming is presented in Sect. 8.
The measurement accuracy of Z and Doppler radial velocity is a function of time to independence (TD), PRF, and SNR (Doviak and Zrnic, 1993). TD determines the interval between two radar measurements that are statistically independent. It is a function of transmit frequency and spectrum width (Bringi and Chandrasekar, 2001). At C band, TD is 6.2 ms for a Doppler spectrum width of 1 m s−1. The beam multiplexing technique allows for a reduction in the dwell time needed to acquire a sufficient number of independent samples. Averaging the signals of independent samples reduces fluctuation in radar estimates of wind and reflectivity. Figure 4 shows contiguous pulses and beam multiplexing pairs. The minimum time to independence interval between beam multiplexing pairs is TD. The maximum allowable dwell time on a radar sampling volume depends on the advection time of the storm. For maximum allowable dwell time of 2.33 s and weather advection of 28.8 m s−1 (60 miles per hour), more than 75 % of weather echo remains in sampling volumes at ranges > 14 km (Curtis, 2009).
Typical scan sequence in less than 2 s time interval would consist of three types of scans: (i) dual Doppler, (ii) dual Doppler and dual polarization, and (iii) surveillance. Dual-Doppler mode will be the primary mode of operation. In this mode, each of the four AESAs will generate a single “pencil” beam that will be scanned in azimuth and elevation. Scanning in azimuth will be between two fixed angles: one fore and one aft. The fore and aft azimuth angles will be separated by 35∘ (Vivekanandan et al., 2014). Each of the 25 elevation angles will be covered with about 25 independent pulse pair radar measurements at each beam position in 1 s. Dual-polarimetric measurements will be collected by transmitting alternatively in horizontal and vertical polarizations in the fore direction in dual-polarization and dual-Doppler scan mode. Polarimetric measurements will be collected only over 10 elevation angles in 0.4 s. A secondary surveillance scan mode of duration 0.4 s will be interleaved every 30 to 60 s periodically with the primary mode to produce a “composite” plan position indicator (PPI) scan which incorporates data from the three aft mounted AESAs and the weather avoidance radar located in the nose of the aircraft. In surveillance mode, the elevation angle is held fixed at 0∘ and the beam is scanned in azimuth.
This section considers three aperture shapes for the AESA and assesses their suitability to APAR. Individual element radiation pattern and array factor determine the radiation pattern of an AESA. Radiation elements could be dipoles, waveguide slots, or microstrip antenna patch. These elements arranged in a plane in rectangular, square, circular, or elliptic shape defines a planar array.
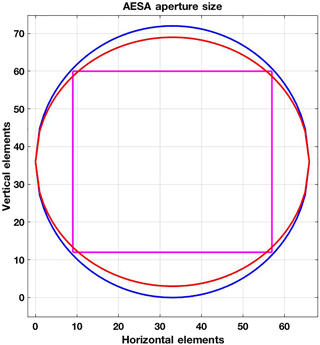
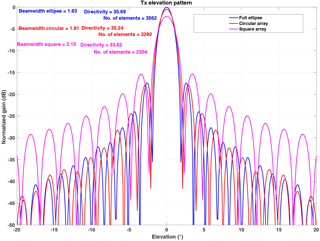
The radiation pattern of a planar array is characterized by directivity, 3 dB beam width, side lobe level, and cross-polar isolation. Radiation characteristics of rectangular, square, and circular planar arrays with crossed dipole element as a radiating element are studied and are depicted in Fig. 5. Available maximum fuselage area for AESA on a C-130 aircraft is elliptically shaped with major and minor axes of 1.93 and 1.78 m, respectively. This area could hold about 3562 radiating elements at half-wavelength spacing. At C-band center frequency of 5.45 GHz, the half-wavelength spacing is 2.75 cm. Figure 6 shows uniformly weighted array factor patterns for the elliptical, circular, and square apertures. The maximum circular area in that elliptic area accommodates 3280 radiating elements whereas a square aperture will hold only 2304 elements. For matched beamwidths in azimuth and elevation, a square or circular aperture is preferred but square aperture would transmit 30 % less power than a circular aperture. Also, for a uniform illumination, the circular aperture has 4 dB lower peak sidelobes than a square aperture.
Figure 7 shows transmit and receive patterns of the circular aperture for three different taperings: (i) uniform tapering for both transmit and receive patterns, (ii) uniform transmit and 30 dB Taylor taper for the receive pattern, and (iii) 15 and 30 dB Taylor tapering of transmit and receive aperture. This is because the two-way antenna pattern is a product of transmit and receive patterns. In transmit and receive modes when all of the planar elements are tapered uniformly maximum sensitivity is realized but peak side lobe (PSL) and integrated sidelobes (ISL) are the highest. Lower PSL and ISL are desired for minimizing spatially disparate targets from biasing the measurement of interest. When transmit and receive apertures are tapered, PSL and ISL are minimum but sensitivity is lower by 1.6 dB when compared to uniform tapering of aperture in transmit and receive modes. As expected, the receiver pattern has a lower sidelobe but its main beam is broader. Typically, in the receive mode nonuniform weighting across planar array is applied for realizing a lower sidelobe and the uniform transmit weighting is applied for realizing maximum-power aperture factor, and the resultant two-way pattern is expected to have a desired lower sidelobe. When receive aperture is tapered 30 dB and maximum power is transmitted by uniform weighting of the aperture, relative sensitivity is decreased only slightly and PSL and ISL are lowered by 8 and 10 dB, respectively.
The limited supply of aircraft power (prime power) available for the phased array system results in very real limitations on radar performance. Prime power for the four AESAs on the NSF/NCAR C-130 is limited to 30 KW. Since the primary mission of airborne weather radar is to sample hydrometeors, scan coverage of the top and bottom AESAs can be limited to 25 km and ground level, respectively. This effectively reduces the combined duty cycle on receive for all four AESAs to ∼ 60 %, thus conserving prime power. Figure 8a provides the radar sensitivity for the three apertures considered, for both ATAR and ATSR TR module architectures and for both 4 and 6 W peak-power HPAs. In several cases, transmit duty cycle was reduced to meet prime-power constraints, resulting in reduced sensitivity at 10 km.
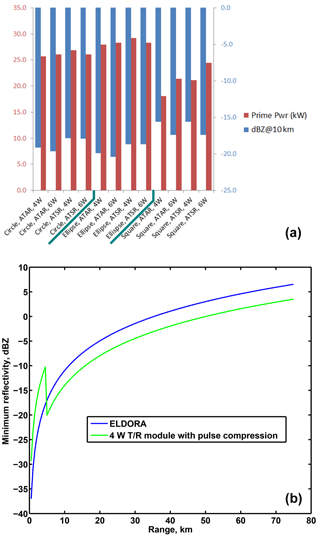
Figure 8(a) Sensitivity comparison for three apertures, using two T/R module architectures (ATAR, ATSR) and two different HPAs (4, 6 W). (b) Sensitivity of APAR as a function of range.
The prime power is estimated based on the preliminary characterization of a “brick” T/R module that has been developed in-house (Salazar et al., 2013). The microwave circuit technology employed in this T/R module is GaAs. The T/R module is comprised of discrete MMICs arranged in an ATAR architecture. The following conclusions can be drawn from this exercise: (i) the square aperture provides the worst sensitivity, (ii) the use of an ATSR architecture results in ∼ 3 dB loss in sensitivity for a given aperture choice, and (iii) the sensitivity of the circular aperture is < 1 dB worse than that of an elliptical aperture operated with the same T/R module architecture and HPA. Figure 8b shows the sensitivity of the APAR as a function of range as depicted by the green curve. The discontinuity in the curve shows the sensitivity difference caused by the transition from short pulse mode to pulse compression mode. In this illustration, the short pulse region extends to 5 km in range and would be ∼ 9 dB less sensitive than the pulse compression region. This sensitivity loss can be mitigated by optimally positioning the aircraft to maximize the sensitivity of the areas of greatest interest. Care must also be taken to merge the data between the two regions, as pulse compression filtering effects can cause artifacts in the data if not handled properly. Long pulse is used, enhancing sensitivity via pulse compression. It is noteworthy that the desired sensitivity of −11 dBZ at 10 km is achievable in either ATSR or ATAR mode in any of the three aperture configurations with 6 or 4 W HPAs.
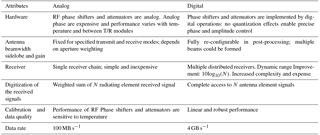
PAR elements could be distinctly configured in three types of architecture: (i) analog, (ii) hybrid (i.e., combination of analog and digital), and (iii) digital. In an analog array RF phase shifters and attenuators are used for steering the beam (Herd and Convey, 2016). The performance of RF components are sensitive to temperature and their precision is limited by the quantization or number of bits that are used to represent phase and attenuation. Beamforming is achieved by summing signals from individual receive elements by an analog combiner. The front-end analog combiner fixes antenna beamwidth and sidelobes and they cannot be modified. In a fully digital array, RF phase shifters and attenuators are replaced by complex multiplication using digital electronics. As digital-electronics-based complex multiplication is relatively immune to quantization effects, precise control of phase and amplitude is realized. Each antenna element is coupled to individual receiver–exciters. In a digital array, an analog-to-digital converter is placed in front end of the every RF element. The received signals are digitized at the element level and they are converted to complex baseband (I/Q) samples.
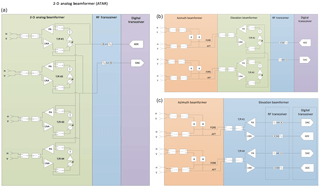
Figure 9APAR architectures for ATAR configuration: (a) 2-D analog, (b) 1-D analog, and (c) 1-D hybrid.
Data rates of fully digital array radar are many orders of magnitude larger than a comparable analog array. An hybrid architecture using a combination of analog and digital beamformer could reduce the date rate to a manageable level for real-time data processing.
Examples of analog, hybrid, and digital array architectures are illustrated in Fig. 9. Analog beamformer using RF phase shifters and attenuators in ATAR configuration is shown Fig. 9a. Beams could be steered to contiguous azimuth and elevation angles. The number of variable phase shifters and attenuators could be reduced by the square root of number of the number of elements by using fixed phase shifters as shown in Fig. 9b. For steering the beam between two discrete beam positions separated by 35∘, fixed phase shifters are used. As alluded to earlier, 2-D winds will be measured using the fore and aft beams separated by 35∘. The antenna beam could be contiguously steered in elevation. The surveillance scan could not be realized in this configuration as the beams could not be steered contiguously in azimuth. Figure 9c shows a hybrid architecture with no variable phase shifters and attenuators. This configuration allows digital beamforming in elevation but does not allow scanning in the azimuthal direction. Table 2 summarizes salient features of analog and digital architectures. Based on the technical specification described in Table 1, the data rate for analog configuration is 100 MB s−1 whereas the digital array radar in 1-D hybrid architecture with no variable phase shifters and attenuators would generate 4 GB s−1 data rate. These data rates are many orders of magnitude larger than a dual-channel polarimetric mechanically scanning radar as S-Pol (Lutz et al., 1997) that generates 8 MB s−1. Since the configuration shown in Fig. 9b and c uses fixed phase shifters for steering the beam in two fixed azimuth directions, they are not capable of scanning in azimuth.
Not having continuous beam steering capability in azimuth limits acquisition of a composite PPI “surveillance” scan from either side of the fuselage radars, which are located on the upper portion of the tail ramp radars in combination with C-130 weather avoidance radar (Vivekanandan et al., 2014). This “surveillance” mode is essential to provide safety in single aircraft missions and will also aid in mission flight planning while in the air. The PAR on top of the fuselage could be operated as an end-fire array for the acquisition of surveillance scan. It should be noted that not having a broadside array on top of the fuselage limits dual-Doppler scans that are suitable for retrieving vertical winds over the head storms. End-fire PAR has lower gain compared to a broadside array. Re-directing the usage of the radar on top of the fuselage would diminish redundancy in APAR's ability to collect volume scans. Instead of a PAR, a mechanically scanning radar as in the NOAA P-3 could provide a dedicated surveillance scan feature. Potential usefulness of end-fire PAR and mechanically scanning radar for surveillance scan application will be investigated in the future. Additional studies are necessary for understanding pros and cons of operating the radar on top of the fuselage in broadside and end-fire configurations.
Weather radar applications place high demands on phased array calibration. It is critical to accurately know the gain, beamwidth, and pointing angle of the array over a variety of operating conditions. Calibration is divided into three phases: (i) characterization, (ii) field calibration, and (iii) end-to-end calibration using an external target such as the sun or a rain medium. Characterization is performed under controlled conditions in an anechoic chamber. It is done prior to the arrays being put in service or after any major component failure or repair. Field calibration is done in situ on the aircraft. It is performed after the arrays are installed on the aircraft prior to a field project or during a field project after a repair has been made. Field calibration must be able to compensate for component drift as well as any performance variations due to the departure of the installation environment from that of the anechoic chamber. The equipment, if any, required for field project calibration must be compact and transportable. The field calibration of a single array must be able to be completed within 10 h, including any setup or teardown of equipment.
Reflectivity can be calibrated using a known signal source such as transmit power from a horn antenna in the far zone or the solar radiation. When a known external signal source is used, the radar does not transmit, and only the receiver system is calibrated. In the case of solar calibration (Tapping, 2001), the receiver should be sensitive enough to detect the low signal power (−100 dBm). Also, the main lobe beam width should be less than 0.5∘ for satisfying the beam-filled condition. In the transmit and receive mode, a highly reflective test sphere suspended from a tethered balloon can be used as a known reference target for calibration. However, the sphere being a point target does not fill the radar beam; as a result, only the on-axis gain of the beam is measured. Self-consistency among Z, ZDR, and KDP can be used for calibrating the radar system (Vivekanandan et al., 2003). One of the advantages of using power and phase measurements from a single radar is the elimination of sampling volume differences among the measurements. At C band, ZHH and ZDR must be corrected for attenuation and differential attenuation prior to calibration based on self-consistency among radar measurements. Attenuation and differential attenuation could be obtained from propagation measurement or a variational method that use both ZDR and KDP measurements (Chang et al., 2014).
In the case of a mechanically steered antenna, the horizontally and vertically polarized beams preserve intrinsic source polarimetric response independent of the beam direction. Since orthogonality between H and V polarization is desired for estimating cloud microphysical measurements of hydrometeors, radiation fields in dual-polarization radar are transmitted orthogonally to each other. In an ESA when a beam is steered electronically away from the boresight, the transmitted field is biased as a function of scan angle and cross coupling between dual-polarization sources occurs (Zhang et al., 2009). Figure 10 illustrates a spherical coordinate system of planar array and hydrometeor scattering location at range r.

Figure 10The coordinate system for electric fields from a pair of microstrip radiating elements. is the magnetic current density of a horizontally polarized radiating element. is the magnetic current density of a vertically polarized radiating element hydrometeors are located at range r. Unit vectors ar, aθ, and aφ form a local orthogonal system at r (Lei et al., 2015).
The relations among transmit polarization field vectors at the planar aperture, incident field vectors on a hydrometeor, and received fields can be described using the following linear transformation. The transmitted electric fields, and , are generated by radiation sources Mh and Mv and projected onto the local H and V directions:
where the projection matrix P is (Lei et al., 2015)
where the superscripts define H and V antenna ports. The H antenna port primarily transmits horizontally polarized fields and V antenna port primarily transmits vertically polarized fields, and all electric fields on the right side of the above equation are normalized by their respective broadside electric fields (e.g., or is normalized by ).
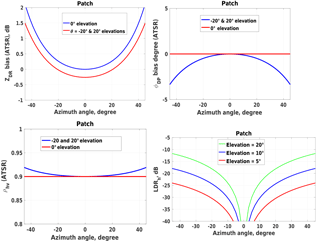
Figure 11Biases in ZDR, ΦDP, ρHV, and LDR as a function azimuth and elevation scan angle of the radar beam.
The projection matrix for microstrip patch antenna is (Lei et al., 2015)
where radiation fields of microwave patch antenna , , and are related to g(h)(θ,ϕ) and g(v)(θ,ϕ) (Balanis, 1997). The projection matrix, P, couples oblique fields Eh and Ev to the local H and V coordinates at the scatterer and at the ESA aperture. The horizontally polarized field is a function of sin(θ) and vertically polarized field is a sum of intrinsic vertically polarized weighted by cos(φ) and a leakage term from cross polarization (V) weighted by cos(θ)sin(φ). The cross-coupling term p21 could be neglected as cross-polarization isolation for a microstrip antenna is typically lower than 20 dB. The backscattered field, Er, in the local H and V directions is a product of Et and backscatter matrix S. The received field Er at the ESA aperture in alignment with H and V channels is a product of P and Er. The backscattering matrix is
where S′ the intrinsic backscatter matrix is
In an ATSR mode alternately transmitted H and V pulses are used for retrieving radial velocity and polarimetric radar estimates. The above matrix is rewritten to take into account the Doppler phase shift between H and V pulse period as
Since the projection matrix term p21 is zero, the individual elements of the received backscatter at the ESA are
In the ATSR mode, this is a set of linear equations (Zrnić et al., 2011). The intrinsic scattering matrix elements are estimated as projection matrix P and to backscatter measurements SP. The element at 2i+1 time interval is related to the element at 2i by the Doppler phase shift . The Doppler shift and ΦDP are estimated from cross correlation between consecutive estimates of co-polarization scattering amplitudes. Unbiased estimates of polarimetric observables require calibrated transmit amplitudes. Thus pulse-pair methods can be used for estimating unbiased Doppler and polarimetric measurements, provided transmit amplitudes are known.
Once the backscatter amplitudes are estimated using the above equations, all of the polarimetric variables could be derived (Zrnić et al., 2011). The bias in polarimetric measurements is estimated for radar resolution volume populated with spherical hydrometeor with a baseline ρhv of 0.9. The estimated bias depends on radiation pattern of the radiating element. The effect of the array factor is not considered in this study.
The bias is estimated for stacked patch microstrip antenna radiation element described in Lei et al. (2015). Figure 11 shows that biases in ZDR, ΦDP, ρhv, and LDR are symmetrical with respect to changes in azimuth and elevation angles. For 0∘ elevation, as the azimuth angle increases, ZDR is positively biased. For both positive and negative elevation angles ZDR is biased negatively and it varies with the azimuth angle. For azimuth and elevation angles < 20∘, the bias is < 0.25 dB. ΦDP and ρhv exhibit no bias for 0∘ elevation and the bias is less than 1∘ for elevation and azimuth angles < 20∘. Bias in ρhv is less than 1 % for elevation angle < 20∘. Bias in LDR significantly increases as the beam scanned away from bore sight. For elevation angle < 5∘ and azimuth angle < 20∘ LDR is < −30 dB.
APAR with dual-polarimetric and dual-Doppler capability allows concurrent estimates of microphysical (e.g., precipitation types and sizes, quantitative precipitation estimation) and 3-D winds in a precipitation system. At present, no other instrument other than an airborne polarimetric Doppler phased array radar system has the potential to estimate 3-D winds and microphysics concurrently. Both ATAR and ATSR polarimetric configurations require the same amount of time for acquiring ZDR, ΦDP, and ρHV. An additional receive channel in ATSR enables measurement of LDR at a faster pace but the ATSR configuration requires twice the amount of receiver elements compared to the ATAR configuration. Multiple AESA radars on the C-130 fuselage enhance spatial and temporal resolutions of measurements. Solid-state, compact T/R elements based on GaAs or GaN is the key enabling technology; only demonstrated hardware and software subsystems will be included in the design of the AESA.
Agile beam steering using the e-scan feature enables the collection of more independent samples in a specified time interval when compared to a mechanically scanning radar. Since an airborne radar has a limited amount of time to collect measurements over a specified sample volume, agile beam steering reduces uncertainty in radar measurements.
For the maximum available area for AESA on a C-130 aircraft, elliptical and circular apertures produce almost the same directivity, but the circular planar array is more desirable. For uniform illumination, the circular aperture has 3 dB lower peak sidelobe than a rectangular or square aperture. Unlike elliptic, square, or rectangular planar arrays, distortions in the array pattern of a circular array due to mutual coupling effect are the same for each element and this makes it easier to deal with the mutual coupling effect. With respect to sensitivity, the elliptical aperture with 6 W HPA offers ∼ 1 dB better sensitivity than the circular aperture and ∼ 3 dB better than the square aperture. Circular aperture offers matched beams in horizontal and vertical polarization transmission.
Phased array radar architecture is evolving toward a combination of analog and digital (hybrid) and fully digital architecture. From the perspective of robust performance, improved data quality, and adaptive beam forming, digital array architecture is preferred. Since digital array radar produces higher data rates, practical requirements for processing high data rates need to be evaluated.
Methodologies for estimating polarimetric observables are summarized based on the earlier published results. Biases in ZDR, ΦDP, ρhv, and LDR due to cross coupling between dual-polarization sources are symmetrical with respect to changes in azimuth and elevation angles and they are with in acceptable range for microphysical studies for azimuth and elevation angles < 20∘. In an alternate transmit mode, the received voltages are a set of linear equations and can be solved either by pulse-to-pulse adjustment or powers and correlations of received voltages. Radial wind and polarimetric observables can be estimated from correlations of received voltages. Self-consistency among ZHH, ZDR, and KDP will be used for absolute calibration of reflectivity. This would require unbiased ZDR and attenuation corrected reflectivity.
The software used in this publication can be obtained by sending an email to vivek@ucar.edu.
| AESA | Active electronically scanned array |
| APAR | Airborne phased array radar |
| ATAR | Alternate transmit and alternate receive |
| ATSR | Alternate transmit and simultaneous receive |
| C-130 | Four-engine turboprop military transport aircraft |
| dBZ | Radar reflectivity factor |
| ELDORA | Electra Doppler radar |
| Electra | Turboprop airliner |
| EOL | Earth Observing Laboratory |
| e-scan | Electronic scanning |
| FPGA | Field-programmable gated array |
| H | Horizontal |
| HPA | High-power amplifier |
| ICPR | Integrated cross-polar ratio |
| KDP | Specific propagation phase |
| LNA | Low noise amplifier |
| LDR | Linear depolarization ratio |
| PA | Power amplifier |
| MMIC | Monolithic microwave integrated circuits |
| NCAR | National Center for Atmospheric Research |
| NOAA | National Oceanic and Atmospheric Administration |
| NSF | National Science Foundation |
| PAR | Phased array radar |
| PPI | Plan position indicator |
| PRF | Pulse repetition frequency |
| P-3 | Four-engine turboprop surveillance aircraft |
| RF | Radio frequency |
| Rx | Receiver |
| SNR | Signal-to-noise ratio |
| STSR | Simultaneously transmit and simultaneously receive |
| TD | Time to independence |
| T/R | Transmit–receive |
| Tx | Transmitter |
| V | Vertical |
| ZHH | Reflectivity |
| ZDR | Differential reflectivity |
| ΦDP | Propagation phase |
The authors declare that they have no conflict of interest.
The National Science Foundation primarily funds NCAR. This material is based
upon work supported by the National Science Foundation under cooperative
grant numbers NSF0015 and MO904552. The authors are grateful to Guifu Zhang
and Lei Lei of University of Oklahoma, Norman, OK, for providing the software
for estimating bias in polarimetric radar observations. Wei-Yu Chang of
Chinese Cultural University, Taipei, Taiwan, performed model computations
shown in Fig. 3. We would also like to acknowledge the contributions of
Bernard Hwang for his work in the redesign and characterization of the T/R
module PCB. The support of Wen-Chau Lee, James Moore, and Peisang Tsai of NCAR
is recognized. Any opinions, findings, and conclusions or recommendations
expressed in this material are those of the author(s) and do not necessarily
reflect the views of the National Science Foundation.
Edited by: Mehrez Zribi
Reviewed by: Jacques
Testud and one anonymous referee
Balanis, C. A.: Antenna theory: analysis and design, 2nd Edn., Wiley, xvi, 941 pp., New Jersey, USA, 1997.
Bluestein, H. B. and Wakimoto, R. M.: Mobile radar observations of severe convective storms, Vol. 52, Meteorological Monographs, American Meteorological Society, 105–136, 2003.
Brandes, E. A., Zhang, G., and Vivekanandan, J.: Comparison of polarimetric radar drop size distribution retrieval algorithms, J. Atmos. Ocean. Tech., 21, 584–598, 2004.
Bringi, V. N. and Chandrasekar, V.: Polarimetric Doppler Weather Radar, Cambridge University Press, New York, 2001.
Bringi, V. N., Chandrasekar, V., Balakrishnan, N., and Zrnić, D.: An Examination of Propagation Effects in Rainfall on Radar Measurements at Microwave Frequencies, J. Atmos. Ocean. Tech., 7, 829–840, 1990.
Clothiaux, E. E., Miller, M. A., Albrecht, B. A., Ackerman, T. P., Verlinde, J., Babb, D. M., Peters, R. M., and Syrett, W. J.: An evaluation of a 94-GHz radar for remote sensing of cloud properties, J. Atmos. Ocean. Tech., 12, 201–229, 1995.
Chang, W., Vivekanandan, J., and Wang, T.-C. C.: Estimation of X-band Polarimetric Radar Attenuation and Measurement Uncertainty Using a Variational Method, J. Appl. Meteorol., 53, 1099–1119, 2014.
Curtis, C. D.: Exploring the capabilities of the agile beam phased array weather radar, PhD Dissertation, University of Oklahoma, 2009.
Doviak, R. J. and Zrnic, D.: Doppler radar and weather observations, Academic Press, San Diego, California, USA, 562 pp., 1993.
Girardin-Gondeau, J., Baudin, F., and Testud, J.: Comparison of various coded waveforms for an airborne meteorological Doppler radar, J. Atmos. Ocean. Tech., 8, 234–246, 1991.
Herd, J. S. and Convey, M. D.: The evolution of modern phased array architecture, P. IEEE, 104, 519–529, 2016.
Hildebrand, P. H., Lee, W.-C., Walther, C. A., Frush, C., Randall, M., Loew, E., Neitzel, R., Parsons, R., Testud, J., Baudin, F., and LeCornec, A.: The ELDORA/ASTRAIA airborne Doppler weather radar: High resolution observations from TOGA COARE, B. Am. Metorol. Soc., 77, 213–232, 1996.
Lhermitte, R.: A 94-GHz Doppler radar for cloud observations, J. Atmos. Ocean. Tech., 4, 36–48, 1987.
Lei, L., Zhang, G., Doviak, R., and Karimkashi, S.: Comparison of theoretical biases in estimating polarimetric properties of precipitation with weather radar using parabolic reflector or planar and cylindrical arrays, IEEE T. Geosci. Remote Sens., 53, 4313–4327, 2015.
Lutz, J., Rilling, B., Wilson, J., Weckwerth, T., and Vivekanandan, J.: S-Pol after three operational deployments, technical performance, siting experiences, and some data examples, Preprints, 28th Conf. on Radar Meteorology, Austin, TX, 7–12 September, Amer. Meteor. Soc., Boston, 286–287, 1997.
Salazar, J. L., Medina, R. H., and Loew, E.: T/R modules for active phased array radars, IEEE Phased array radar conference, Waltham, MA, 2013.
Smith, R. B., Carbone, R. E., and Zeng, X.: The lower atmospheric observing facilities workshop – meeting the challenges of climate system sciences, 18–19 June 2012, Boulder, CO, USA, 44 pp., available at: https://www.eol.ucar.edu/system/files/LAOF_Workshop_Report_FINAL_06112013.pdf (last access: January 2018), 2012.
Tapping, K.: Antenna calibration using the 10.7 cm solar flux. Preprints, Workshop on Radar Calibration, Albuquerque, NM, 13–14 January, Amer. Meteor. Soc., Boston, 32 pp., 2001.
Vivekanandan, J., Zhang, G., Ellis, S. M., Rajopadhyaya, D., and Avery, S. K.: Radar reflectivity calibration using differential propagation phase measurement, Radio Sci., 38, 8049, https://doi.org/10.1029/2002RS002676, 2003.
Vivekanandan, J., Zhang, G. F., and Brandes, E. A.: Polarimetric radar estimators based on a constrained gamma drop size distribution model. J. Appl. Meteorol., 43, 217–230, 2004.
Vivekanandan, J., Lee, W.-C., Loew, E., Salazar, J. L., Grubišic, V., Moore, J., and Tsai, P.: The next generation airborne polarimetric Doppler weather radar, Geosci. Instrum. Method. Data Syst., 3, 111–126, https://doi.org/10.5194/gi-3-111-2014, 2014.
Wang, H., Fang, D., and Chow, Y. L.: Grating lobe reduction in a phased array of limited scanning, IEEE Trans. Antenn. Propag., 56, 1581–1585, 2008.
Wang, Y. and Chandrasekar, V.: Polarization isolation requirements for linear dual-polarization weather radar in simultaneous transmission mode of operation, IEEE T. Geosci. Remote Sens., 44, 2019–2028, 2006.
Weber, M. E., Cho, J. Y. N., Herd, J. S., Flavin, J. M., Benner, W. E., and Torok, G. S.: The Next-Generation Multimission U.S. Surveillance Radar Network, B. Am. Meteorol. Soc., 88, 1739–1751, 2007.
Yu, T.-Y., Orescanin, M. B., Curtis, C. D., Zrnić, D. S., and Forsyth, D. E.: Beam multiplexing using the phased-array weather radar, J. Atmos. Ocean. Tech., 24, 616–626, 2007.
Zhang, G.: Weather Radar Polarimetry, Boca Raton, CRC Press, 253–277, 2017.
Zhang, G., Doviak, R. J., Zrnić, D. S., Crain, J., Staiman, D., and Al-Rashid, Y.: Phased array radar polarimetry for weather sensing: A theoretical formulation for bias corrections, IEEE T. Geosci. Remote Sens., 47, 3679–3689, 2009.
Zrnić, D. S., Zhang, G., and Doviak, R. J.: Bias correction and Doppler measurement for polarimetric phased-array Radar, IEEE T. Geosci. Remote Sens., 49, 843–853, 2011.
- Abstract
- Introduction
- System description
- Transmit frequency
- Polarimetric measurement configurations
- Agile beam scanning
- APAR antenna aperture
- Radar sensitivity and prime power
- Radar architecture
- Calibration of reflectivity
- Removal of bias in polarimetric radar measurements
- Summary
- Code and data availability
- Appendix A: List of acronyms
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- System description
- Transmit frequency
- Polarimetric measurement configurations
- Agile beam scanning
- APAR antenna aperture
- Radar sensitivity and prime power
- Radar architecture
- Calibration of reflectivity
- Removal of bias in polarimetric radar measurements
- Summary
- Code and data availability
- Appendix A: List of acronyms
- Competing interests
- Acknowledgements
- References