the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
How many solar wind data are sufficient for accurate fluxgate magnetometer offset determinations?
Ferdinand Plaschke
Accurate magnetic field measurements by fluxgate magnetometers onboard spacecraft require ground and regular in-flight calibration activities. Therewith, the parameters of a coupling matrix and an offset vector are adjusted; they are needed to transform raw magnetometer outputs into calibrated magnetic field measurements. The components of the offset vector are typically determined by analyzing Alfvénic fluctuations in the solar wind if solar wind measurements are available. These are characterized by changes in the field components, while the magnetic field modulus stays constant. In this paper, the following question is answered: how many solar wind data are sufficient for accurate fluxgate magnetometer offset determinations? It is found that approximately 40 h of solar wind data are sufficient to achieve offset accuracies of 0.2 nT, and about 20 h suffice for accuracies of 0.3 nT or better if the magnetometer offsets do not drift within these time intervals and if the spacecraft fields do not vary at the sensor position. Offset determinations with uncertainties lower than 0.1 nT, however, would require at least hundreds of hours of solar wind data.
In situ investigations of the plasma environments of planets, moons, comets, or other solar system bodies require magnetic field measurements by spacecraft magnetometers. Typically, fluxgate magnetometers are used for scientific applications. The required measurements can only be provided if those magnetometers are accurately calibrated. This means that a coupling matrix C and an offset vector O have to be accurately known in order to transform raw magnetometer outputs Braw into calibrated magnetic field measurements B (e.g., Fornaçon et al., 1999; Balogh et al., 2001; Auster et al., 2008):
Both C and O should be determined on the ground and in flight, as calibration parameters, in particular the offset components, are known to change over time. Offset changes may be associated with instrument drifts or with variations of the spacecraft-generated magnetic fields at the magnetometer sensor, as the offsets are the outputs of a magnetometer in vanishing ambient field conditions.
If the spacecraft is spin stabilized, then the spin plane offset components are easily determined by minimizing the spin tone content in the despun spin plane magnetic field measurements (e.g., Farrell et al., 1995; Kepko et al., 1996; Plaschke et al., 2019). If the spacecraft is non-spinning, i.e., three-axis stabilized, then the following methods can be used for offset determination: (1) Alfvénic fluctuations that are abundant in the solar wind are characterized by changes in the magnetic field components, while the field magnitude stays constant. An analysis of such fluctuations allows for an adjustment of the offsets through minimization of the changes in the magnetic field magnitude (e.g., Belcher, 1973; Hedgecock, 1975; Leinweber et al., 2008). This is the typical method for offset determination if solar wind measurements are available. (2) Compressional fluctuations can also be used to determine magnetometer offsets through the application of the mirror-mode method (Plaschke and Narita, 2016; Plaschke et al., 2017). In this case the fact that the maximum variance direction of the fluctuations should coincide with the average magnetic field direction is used. Any mismatch may be attributed to incorrect offsets. (3) Furthermore, offsets may be obtained by comparing fluxgate magnetometer magnetic field measurements to (i) measurements from an electron drift instrument (EDI) or from an absolute magnetometer (Georgescu et al., 2006; Nakamura et al., 2014; Plaschke et al., 2014), (ii) otherwise known fields, e.g., when the spacecraft is in a diamagnetic cavity (Goetz et al., 2016a, b), or (iii) field estimates from a field model such as the International Geomagnetic Reference Field (e.g., Thébault et al., 2015).
This paper deals with option (1). It shall address the following question: how many solar wind data are needed to obtain all three components of the offset vector with a certain accuracy? It shall be assumed that the magnetometer is otherwise perfectly calibrated (C accurately determined), that the offset components are not drifting (i.e., non-drifting instrument and non-varying spacecraft fields at the magnetometer sensor position), and that the magnetometer is mounted on a non-spinning spacecraft. The latter assumption means that the spacecraft spin cannot be used to support the determination of the spin plane offset components.
To answer the question posed in the Introduction, well-calibrated magnetometer measurements in the solar wind are needed. In this paper, measurements from the National Aeronautics and Space Administration (NASA) Magnetospheric Multiscale (MMS) mission are used (Burch et al., 2016). The mission consists of four spin-stabilized spacecraft launched on 13 March 2015 into highly elliptical and roughly equatorial orbits. The goal of the mission is to explore the small-scale physics of magnetic reconnection. To achieve this goal, the spacecraft are required to fly in close configuration (spacecraft separations down to a few kilometers) in regions where reconnection is likely to take place, at the dayside magnetopause and in the geomagnetic tail. Due to the small spacecraft separations, high-cadence measurements and the most accurate calibrations of all instruments are key. Otherwise, differences between spacecraft cannot be resolved.
The MMS spacecraft are equipped with instruments to measure particle distribution functions (Pollock et al., 2016; Young et al., 2016; Mauk et al., 2016; Blake et al., 2016; Torkar et al., 2016) as well as electric and magnetic fields (Torbert et al., 2016a; Russell et al., 2016; Le Contel et al., 2016; Ergun et al., 2016; Lindqvist et al., 2016; Torbert et al., 2016b). Here, only measurements by the MMS fluxgate magnetometers (FGMs) are used. Each spacecraft has two fluxgate magnetometers, an analog fluxgate and a digital fluxgate magnetometer (AFG and DFG), mounted at the ends of two separate 5 m long booms (Torbert et al., 2016a; Russell et al., 2016). The instruments and, in particular, the offsets pertaining to AFG and DFG on all spacecraft are very well calibrated: as the MMS spacecraft are spinning, the spin plane offsets can be and are dynamically adjusted in low fields, e.g., in the solar wind (Bromund et al., 2016; Plaschke et al., 2019). Thereby, temperature-dependent offset variations on the order of 0.2 nT are corrected. As a result, the absolute uncertainties of the magnetic field measurements in the spin plane components can realistically be assumed to be on the order of some 10 pT. The spin axis offsets are updated once per orbit by comparison with MMS EDI measurements (Plaschke et al., 2014; Torbert et al., 2016b). The accuracy of this offset determination is on the order of 0.1 nT. Unfortunately, the comparison of EDI and FGM measurements cannot be performed continuously. Hence, the spin axis offsets cannot be dynamically adjusted. As they are likely to drift by 0.2 nT, just as the spin plane offsets do, the absolute uncertainties pertaining to the spin axis components can realistically be assumed to be on the same order of 0.2 to maximally 0.3 nT. Due to the small spacecraft separations, inter-spacecraft and inter-instrument (AFG versus DFG) comparisons allow for further fine tuning in the spin axis offsets. Any additional spin plane or spin axis offsets determined from these data should ideally vanish within the uncertainty limits (spin plane: some 10 pT; spin axis: 0.2 to 0.3 nT). Deviations from 0 above those uncertainty levels are hence indicative of the accuracy of the offset determinations.
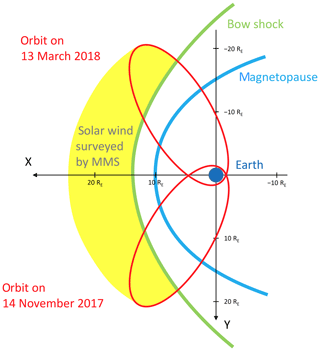
Figure 1Sketch of the MMS extended mission phase 3B orbits between 14 November 2017 and 13 March 2018. Locations where MMS surveyed the solar wind in that phase are displayed in yellow. The Sun is to the left.
Long-duration solar wind measurements are obtained by MMS during the extended mission phase, when the MMS orbit apogees are located dayside of the terminator at distances of 25 RE (Earth radii) from the Earth's center. The perigee distances in this phase are just over 1000 km above the ground (see Fig. 1). Fully calibrated MMS 1 FGM survey mode data (AFG measurements) from the dayside extended mission phase 3B (14 November 2017 to 13 March 2018, i.e., 119 days) are used in despun major principal axis (DMPA) coordinates. In this coordinate system, the major principal axis of inertia (i.e., the spin axis) points in the z direction and the spacecraft–Sun vector lies in the x–z plane. The DMPA system is closely aligned with the geocentric solar ecliptic (GSE) system, as the spin axis (z) points essentially normal to the ecliptic and the spacecraft–Sun vector almost coincides with the DMPA x axis. The data are available in 16 Hz resolution. Alfvénic fluctuations in the solar wind are of significantly lower frequency. Therefore, the data are resampled to 1 Hz to reduce computational efforts.
The data are subdivided into 171 360 nonoverlapping 1 min intervals. Note that 1 min is a multiple of the spacecraft spin period of 20 s (Tooley et al., 2016). Solar wind intervals are easily identified by nT: Ntot= 116 914 intervals fulfill this criterion. For each of these intervals, 3-D offset vector estimates O are determined by minimization of the standard deviation of , a variant of the Davis–Smith method (Davis and Smith, 1968; Belcher, 1973). Offset components Ox, Oy, and Oz are required to be within ±10 nT around 0. This is fulfilled in NO= 68 324 cases. This offset criterion selects intervals containing Alfvénic fluctuations. In these cases, a minimum of the standard deviation of can be found for small offset corrections O. In contrast, if there are compressional fluctuations, maximizing the offset component in the minimum variance direction will yield the smallest standard deviations of . But then at least one component of O is likely to be found outside ±10 nT, or no convergence is found on any O vector.
For an offset component estimate to be meaningful (e.g., Ox), the magnetic field in that component (e.g., Bx) should be fluctuating during the 1 min interval of interest. Hence, offset components pertaining to intervals are selected for which the standard deviations σ of the respective component of B are larger than a certain threshold σc. The numbers N of intervals selected are shown in Fig. 2a. N(σc= 0) is obviously NO= 68 324 for all x, y, and z components (shown in blue, green, and red, respectively); N decreases if higher threshold values σc are used. This decrease is not exactly the same for all components. Apparently, magnetic field fluctuations in Bx are slightly weaker than in the other components so that for any given σc≠0. Note that the DMPA x component corresponds to the radial direction to the Sun, which has previously been reported to feature lower levels of fluctuations (Belcher, 1973).

Figure 2(a) Numbers N of 1 min intervals selected when using the threshold σc on component standard deviations σ in the magnetic field; N pertaining to x, y, and z components shown in blue, green, and red, respectively. (b) Minutes of solar wind data T required to obtain one selected interval as a function of σc, derived from x component N(σc) values.
The numbers N are fractions of all 1 min intervals of solar wind data Ntot, where nT. Furthermore, using magnetic field data from NASA's OMNI high-resolution data set (King and Papitashvili, 2005) for the same period of time (14 November 2017 to 13 March 2018), it is possible to obtain the fraction of solar wind with nT: it is 88.4 %. Therewith, it is possible to compute the number of solar wind measurements (T in minutes) required to obtain one interval featuring an offset estimate within ±10 nT and σ>σc in a magnetic field component:
This function T(σc) is shown in Fig. 2b. If σc=0.5 nT, then obtaining one suitable offset estimate in any component requires almost 10 min of solar wind measurements.
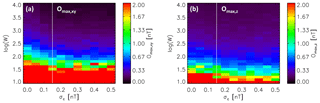
Figure 3Offset uncertainties Omax,xy (a) and Omax,z (b) as a function of σc and W. White vertical lines mark σc=0.15 nT in both panels.
Note that the OMNI solar wind data set from NASA's Goddard Space Flight Center (GSFC) is based on measurements by different solar wind monitors (e.g., the Advanced Composition Explorer (ACE) and the Wind spacecraft). These measurements are propagated in time to represent observations at the Earth's bow shock nose. The OMNI data set pertains to and is distributed by the NASA/GSFC Space Physics Data Facility.
The offset estimates from any particular selected interval are almost certainly not accurate, but a sample of those intervals can yield an accurate offset. From W offsets pertaining to one component (x, y, or z) from intervals with σ>σc, a final offset Of can be computed by using the kernel density estimator (KDE) method. From the W offsets (index: i=1…W), a probability density function P can be determined as follows (e.g., Plaschke and Narita, 2016):
The parameter h is a bandwidth set to 1 nT. Then where P maximizes.
For σc=0…0.5 nT, W=10… 10 000 offsets from each component are randomly selected 1000 times from the available N(σc) samples. Hence, for each combination of σc and W, 1000 estimates (index j=1…1000) of , , and are computed. The maximum offsets (deviations from 0) pertaining to the spin plane (x and y) and spin axis (z) components are stored separately.
These are the upper-limit estimates of the uncertainty in offset determination in the spin plane and spin axis components. The values of Omax,xy and Omax,z are displayed in Fig. 3; they top out at 2 nT. The minima of Omax,xy and Omax,z are 0.05 and 0.12 nT, respectively. Unsurprisingly, larger sample sizes W of offset estimates yield more accurate offsets, i.e., lower uncertainties Omax. Furthermore, for constant W, both Omax,xy and Omax,z decrease if σc is increased. No improvement in Omax,xy is apparent, however, for σc>0.15 nT. This limit is marked by white vertical lines in both panels of Fig. 3.
The more offset estimates W from 1 min intervals are used, the more solar wind measurements are required to obtain them in the first place. Multiplying T(σc) by W yields the minimum solar wind measurement time. It is displayed in Fig. 4. The minimum TW is just over 19 min (for σc=0 nT and W=10) and the maximum TW in the figure, just over 1600 h, pertains to σc=0.5 nT and W=10 000.
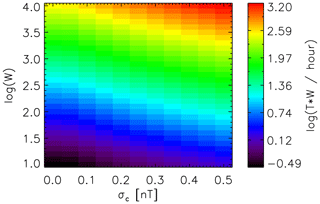
Figure 4Required solar wind measurement time T(σc) W to obtain W offset estimates from intervals with σ>σc, from which final offsets may be computed in all components.
From the data underlying both figures it is possible to find the lowest required solar wind measurement times TW for given as follows: find all combinations of σc and W in Fig. 3 (panel a or b) fulfilling . From those combinations, identify the one associated with the lowest time TW in Fig. 4. The identified parameters σc and W, as well as the minimum times TW, are shown for different limits Omax,c applied to Omax,xy (Fig. 3a) in Table 1. Here, Omax,c is a threshold value for the uncertainty in the offset determination.
Table 1Optimal parameters σc and W as well as minimum solar wind measurement times TW to achieve offset uncertainties based on Omax,xy values shown in Fig. 3a.
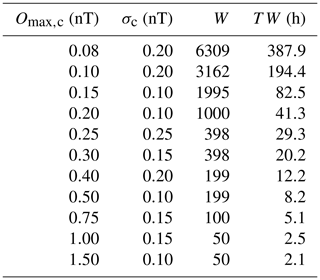
As can be seen in Table 1, σc=0.15 nT seems to be an optimal choice. This is already visible in Fig. 3a, where Omax,xy values appear to stay relatively constant for σc≥0.15 nT but are noticeably larger for lower threshold values. For σc=0.15 nT, Omax,xy and Omax,z values are shown as a function of W or, alternatively, TW in Fig. 5 in blue and red, respectively. They are cuts of Fig. 3a and b along the vertical white lines.
Figure 5 shows that the determination of DMPA z component offsets with a certain accuracy (>0.3 nT) requires fewer solar wind data than the determination of x or y component offsets. The reason might be the use of Alfvénic, i.e., transverse, fluctuations of the solar wind magnetic field. As that field is typically lying in the ecliptic x–y plane (Parker spiral interplanetary magnetic field), the transverse fluctuations will be most apparent in the normal z component (Belcher, 1973). Accuracies better than 0.2 nT are, however, easier to achieve for the spin plane x and y components due to the 0.2 to 0.3 nT uncertainty and variability in the MMS spin axis offsets. Note that the σc=0.15 nT limit does not seem to be related to this uncertainty, as it is more visible in the Omax,xy than in the Omax,z results presented in Fig. 3a and b, respectively. Instead, it may be hypothesized that the optimal choice of σc is rather related to typical fluctuation amplitudes of the solar wind magnetic field.
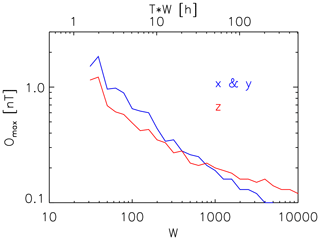
Figure 5Offset uncertainties Omax,xy (blue) and Omax,z (red) as a function of W or TW for fixed σc=0.15 nT.
Values of nT should be unaffected by x and y component calibration uncertainties of some 10 pT. Hence, with the help of Table 1 and Fig. 5 (blue line), both showing Omax,xy results, it is possible to give an answer to the question posed in the Introduction section: how many solar wind data are needed to obtain all three components of the offset vector with a certain accuracy?
Offset determinations with uncertainties better than nT are possible based on less than 2 days (41.3 h) of solar wind measurements. If only 20.2 h of data are available, then offsets may be determined more accurately than nT. Ensuring uncertainties to be on the order of or less than nT, however, may require prohibitively long solar wind measurement intervals of several hundred hours, over which the instrument offsets and spacecraft fields at the magnetometer sensor need to stay constant to within Omax,c. Otherwise, intrinsic offset drifts and field variations over time would limit the attainable accuracy irrespective of the amount of solar wind data used.
Although MMS 1 data are used as a high-quality standard to ascertain the accuracy of the offset determination with the outlined method, the results shown in Table 1 and Fig. 5 (blue line) should not be MMS specific. They should be applicable to any magnetometer–spacecraft configuration, as long as spacecraft-generated magnetic field variations within 1 min intervals are of significantly lower amplitude in the magnetometer data than the natural magnetic field variations of solar wind Alfvénic fluctuations. Those spacecraft-generated field variations may be sufficiently reduced by making use of double-sensor gradiometer measurements.
MMS FGM level 2 survey data are publicly available at https://lasp.colorado.edu/mms/sdc/public (last access: 30 January 2019). OMNI high-resolution solar wind data are publicly available at https://omniweb.gsfc.nasa.gov (last access: 30 January 2019).
The author declares that there is no conflict of interest.
The dedication and expertise of the Magnetospheric Multiscale (MMS) development and operations teams are greatly appreciated. The use of level 2 survey fluxgate magnetometer (FGM) data is acknowledged. The use of the NASA/GSFC Space Physics Data Facility OMNIWeb service and OMNI data is acknowledged.
This work is financially supported by the Austrian Space Applications Programme (ASAP) at the Austrian Research Promotion Agency (FFG), ASAP 14 MERMAG-4, under contract 865967.
This paper was edited by Marina Díaz-Michelena and reviewed by two anonymous referees.
Auster, H. U., Glassmeier, K. H., Magnes, W., Aydogar, O., Baumjohann, W., Constantinescu, D., Fischer, D., Fornaçon, K. H., Georgescu, E., Harvey, P., Hillenmaier, O., Kroth, R., Ludlam, M., Narita, Y., Nakamura, R., Okrafka, K., Plaschke, F., Richter, I., Schwarzl, H., Stoll, B., Valavanoglou, A., and Wiedemann, M.: The THEMIS Fluxgate Magnetometer, Space Sci. Rev., 141, 235–264, https://doi.org/10.1007/s11214-008-9365-9, 2008. a
Balogh, A., Carr, C. M., Acuña, M. H., Dunlop, M. W., Beek, T. J., Brown, P., Fornacon, K.-H., Georgescu, E., Glassmeier, K.-H., Harris, J., Musmann, G., Oddy, T., and Schwingenschuh, K.: The Cluster Magnetic Field Investigation: overview of in-flight performance and initial results, Ann. Geophys., 19, 1207–1217, https://doi.org/10.5194/angeo-19-1207-2001, 2001. a
Belcher, J. W.: A variation of the Davis-Smith method for in-flight determination of spacecraft magnetic fields, J. Geophys. Res., 78, 6480–6490, https://doi.org/10.1029/JA078i028p06480, 1973. a, b, c, d
Blake, J. B., Mauk, B. H., Baker, D. N., Carranza, P., Clemmons, J. H., Craft, J., Crain, W. R., Crew, A., Dotan, Y., Fennell, J. F., Friedel, R. H., Friesen, L. M., Fuentes, F., Galvan, R., Ibscher, C., Jaynes, A., Katz, N., Lalic, M., Lin, A. Y., Mabry, D. M., Nguyen, T., Pancratz, C., Redding, M., Reeves, G. D., Smith, S., Spence, H. E., and Westlake, J.: The Fly's Eye Energetic Particle Spectrometer (FEEPS) Sensors for the Magnetospheric Multiscale (MMS) Mission, Space Sci. Rev., 199, 309–329, https://doi.org/10.1007/s11214-015-0163-x, 2016. a
Bromund, K. R., Plaschke, F., Strangeway, R. J., Anderson, B. J., Huang, B. G., Magnes, W., Fischer, D., Nakamura, R., Leinweber, H. K., Russell, C. T., Baumjohann, W., Chutter, M., Torbert, R. B., Le, G., Slavin, J. A., and Kepko, L.: In-Flight Calibration Methods for Temperature-Dependendent Offsets in the MMS Fluxgate Magnetometers, in: AGU Fall Meeting Abstracts, SM21A–2455, 2016. a
Burch, J. L., Moore, T. E., Torbert, R. B., and Giles, B. L.: Magnetospheric Multiscale Overview and Science Objectives, Space Sci. Rev., 199, 5–21, https://doi.org/10.1007/s11214-015-0164-9, 2016. a
Davis, L. and Smith, E. J.: The in-flight determination of spacecraft field zeros, EOS Trans. AGU, 49, 57–375, https://doi.org/10.1029/TR049i001p00057, 1968. a
Ergun, R. E., Tucker, S., Westfall, J., Goodrich, K. A., Malaspina, D. M., Summers, D., Wallace, J., Karlsson, M., Mack, J., Brennan, N., Pyke, B., Withnell, P., Torbert, R., Macri, J., Rau, D., Dors, I., Needell, J., Lindqvist, P.-A., Olsson, G., and Cully, C. M.: The Axial Double Probe and Fields Signal Processing for the MMS Mission, Space Sci. Rev., 199, 167–188, https://doi.org/10.1007/s11214-014-0115-x, 2016. a
Farrell, W. M., Thompson, R. F., Lepping, R. P., and Byrnes, J. B.: A method of calibrating magnetometers on a spinning spacecraft, IEEE T. Magn., 31, 966–972, https://doi.org/10.1109/20.364770, 1995. a
Fornaçon, K.-H., Auster, H. U., Georgescu, E., Baumjohann, W., Glassmeier, K.-H., Haerendel, G., Rustenbach, J., and Dunlop, M.: The magnetic field experiment onboard Equator-S and its scientific possibilities, Ann. Geophys., 17, 1521–1527, https://doi.org/10.1007/s00585-999-1521-3, 1999. a
Georgescu, E., Vaith, H., Fornaçon, K.-H., Auster, U., Balogh, A., Carr, C., Chutter, M., Dunlop, M., Foerster, M., Glassmeier, K.-H., Gloag, J., Paschmann, G., Quinn, J., and Torbert, R.: Use of EDI time-of-flight data for FGM calibration check on CLUSTER, in: Cluster and Double Star Symposium, vol. 598, ESA Special Publicatio, 2006. a
Goetz, C., Koenders, C., Hansen, K. C., Burch, J., Carr, C., Eriksson, A., Frühauff, D., Güttler, C., Henri, P., Nilsson, H., Richter, I., Rubin, M., Sierks, H., Tsurutani, B., Volwerk, M., and Glassmeier, K. H.: Structure and evolution of the diamagnetic cavity at comet 67P/Churyumov-Gerasimenko, Mon. Not. R. Astron. Soc., 462, S459–S467, https://doi.org/10.1093/mnras/stw3148, 2016a. a
Goetz, C., Koenders, C., Richter, I., Altwegg, K., Burch, J., Carr, C., Cupido, E., Eriksson, A., Güttler, C., Henri, P., Mokashi, P., Nemeth, Z., Nilsson, H., Rubin, M., Sierks, H., Tsurutani, B., Vallat, C., Volwerk, M., and Glassmeier, K.-H.: First detection of a diamagnetic cavity at comet 67P/Churyumov-Gerasimenko, Astron. Astrophys., 588, A24, https://doi.org/10.1051/0004-6361/201527728, 2016b. a
Hedgecock, P. C.: A correlation technique for magnetometer zero level determination, Space Sci. Instrum., 1, 83–90, 1975. a
Kepko, E. L., Khurana, K. K., Kivelson, M. G., Elphic, R. C., and Russell, C. T.: Accurate determination of magnetic field gradients from four point vector measurements, I. Use of natural constraints on vector data obtained from a single spinning spacecraft, IEEE T. Magn., 32, 377–385, https://doi.org/10.1109/20.486522, 1996. a
King, J. H. and Papitashvili, N. E.: Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data, J. Geophys. Res., 110, A02104, https://doi.org/10.1029/2004JA010649, 2005. a
Le Contel, O., Leroy, P., Roux, A., Coillot, C., Alison, D., Bouabdellah, A., Mirioni, L., Meslier, L., Galic, A., Vassal, M. C., Torbert, R. B., Needell, J., Rau, D., Dors, I., Ergun, R. E., Westfall, J., Summers, D., Wallace, J., Magnes, W., Valavanoglou, A., Olsson, G., Chutter, M., Macri, J., Myers, S., Turco, S., Nolin, J., Bodet, D., Rowe, K., Tanguy, M., and de la Porte, B.: The Search-Coil Magnetometer for MMS, Space Sci. Rev., 199, 257–282, https://doi.org/10.1007/s11214-014-0096-9, 2016. a
Leinweber, H. K., Russell, C. T., Torkar, K., Zhang, T. L., and Angelopoulos, V.: An advanced approach to finding magnetometer zero levels in the interplanetary magnetic field, Meas. Sci. Technol., 19, 055104, https://doi.org/10.1088/0957-0233/19/5/055104, 2008. a
Lindqvist, P.-A., Olsson, G., Torbert, R. B., King, B., Granoff, M., Rau, D., Needell, G., Turco, S., Dors, I., Beckman, P., Macri, J., Frost, C., Salwen, J., Eriksson, A., Åhlén, L., Khotyaintsev, Y. V., Porter, J., Lappalainen, K., Ergun, R. E., Wermeer, W., and Tucker, S.: The Spin-Plane Double Probe Electric Field Instrument for MMS, Space Sci. Rev., 199, 137–165, https://doi.org/10.1007/s11214-014-0116-9, 2016. a
Mauk, B. H., Blake, J. B., Baker, D. N., Clemmons, J. H., Reeves, G. D., Spence, H. E., Jaskulek, S. E., Schlemm, C. E., Brown, L. E., Cooper, S. A., Craft, J. V., Fennell, J. F., Gurnee, R. S., Hammock, C. M., Hayes, J. R., Hill, P. A., Ho, G. C., Hutcheson, J. C., Jacques, A. D., Kerem, S., Mitchell, D. G., Nelson, K. S., Paschalidis, N. P., Rossano, E., Stokes, M. R., and Westlake, J. H.: The Energetic Particle Detector (EPD) Investigation and the Energetic Ion Spectrometer (EIS) for the Magnetospheric Multiscale (MMS) Mission, Space Sci. Rev., 199, 471–514, https://doi.org/10.1007/s11214-014-0055-5, 2016. a
Nakamura, R., Plaschke, F., Teubenbacher, R., Giner, L., Baumjohann, W., Magnes, W., Steller, M., Torbert, R. B., Vaith, H., Chutter, M., Fornaçon, K.-H., Glassmeier, K.-H., and Carr, C.: Interinstrument calibration using magnetic field data from the flux-gate magnetometer (FGM) and electron drift instrument (EDI) onboard Cluster, Geosci. Instrum. Method. Data Syst., 3, 1–11, https://doi.org/10.5194/gi-3-1-2014, 2014. a
Plaschke, F. and Narita, Y.: On determining fluxgate magnetometer spin axis offsets from mirror mode observations, Ann. Geophys., 34, 759–766, https://doi.org/10.5194/angeo-34-759-2016, 2016. a, b
Plaschke, F., Nakamura, R., Leinweber, H. K., Chutter, M., Vaith, H., Baumjohann, W., Steller, M., and Magnes, W.: Flux-gate magnetometer spin axis offset calibration using the electron drift instrument, Meas. Sci. Technol., 25, 105008, https://doi.org/10.1088/0957-0233/25/10/105008, 2014. a, b
Plaschke, F., Goetz, C., Volwerk, M., Richter, I., Frühauff, D., Narita, Y., Glassmeier, K.-H., and Dougherty, M. K.: Fluxgate magnetometer offset vector determination by the 3D mirror mode method, Mon. Not. R. Astron. Soc., 469, S675–S684, https://doi.org/10.1093/mnras/stx2532, 2017. a
Plaschke, F., Auster, H.-U., Fischer, D., Fornaçon, K.-H., Magnes, W., Richter, I., Constantinescu, D., and Narita, Y.: Advanced calibration of magnetometers on spin-stabilized spacecraft based on parameter decoupling, Geosci. Instrum. Method. Data Syst., 8, 63–76, https://doi.org/10.5194/gi-8-63-2019, 2019. a, b
Pollock, C., Moore, T., Jacques, A., Burch, J., Gliese, U., Saito, Y., Omoto, T., Avanov, L., Barrie, A., Coffey, V., Dorelli, J., Gershman, D., Giles, B., Rosnack, T., Salo, C., Yokota, S., Adrian, M., Aoustin, C., Auletti, C., Aung, S., Bigio, V., Cao, N., Chandler, M., Chornay, D., Christian, K., Clark, G., Collinson, G., Corris, T., De Los Santos, A., Devlin, R., Diaz, T., Dickerson, T., Dickson, C., Diekmann, A., Diggs, F., Duncan, C., Figueroa-Vinas, A., Firman, C., Freeman, M., Galassi, N., Garcia, K., Goodhart, G., Guererro, D., Hageman, J., Hanley, J., Hemminger, E., Holland, M., Hutchins, M., James, T., Jones, W., Kreisler, S., Kujawski, J., Lavu, V., Lobell, J., LeCompte, E., Lukemire, A., MacDonald, E., Mariano, A., Mukai, T., Narayanan, K., Nguyan, Q., Onizuka, M., Paterson, W., Persyn, S., Piepgrass, B., Cheney, F., Rager, A., Raghuram, T., Ramil, A., Reichenthal, L., Rodriguez, H., Rouzaud, J., Rucker, A., Saito, Y., Samara, M., Sauvaud, J.-A., Schuster, D., Shappirio, M., Shelton, K., Sher, D., Smith, D., Smith, K., Smith, S., Steinfeld, D., Szymkiewicz, R., Tanimoto, K., Taylor, J., Tucker, C., Tull, K., Uhl, A., Vloet, J., Walpole, P., Weidner, S., White, D., Winkert, G., Yeh, P.-S., and Zeuch, M.: Fast Plasma Investigation for Magnetospheric Multiscale, Space Sci. Rev., 199, 331–406, https://doi.org/10.1007/s11214-016-0245-4, 2016. a
Russell, C. T., Anderson, B. J., Baumjohann, W., Bromund, K. R., Dearborn, D., Fischer, D., Le, G., Leinweber, H. K., Leneman, D., Magnes, W., Means, J. D., Moldwin, M. B., Nakamura, R., Pierce, D., Plaschke, F., Rowe, K. M., Slavin, J. A., Strangeway, R. J., Torbert, R., Hagen, C., Jernej, I., Valavanoglou, A., and Richter, I.: The Magnetospheric Multiscale Magnetometers, Space Sci. Rev., 199, 189–256, https://doi.org/10.1007/s11214-014-0057-3, 2016. a, b
Thébault, E., Finlay, C. C., Beggan, C. D., Alken, P., Aubert, J., Barrois, O., Bertrand, F., Bondar, T., Boness, A., Brocco, L., Canet, E., Chambodut, A., Chulliat, A., Coïsson, P., Civet, F., Du, A., Fournier, A., Fratter, I., Gillet, N., Hamilton, B., Hamoudi, M., Hulot, G., Jager, T., Korte, M., Kuang, W., Lalanne, X., Langlais, B., Léger, J.-M., Lesur, V., Lowes, F. J., Macmillan, S., Mandea, M., Manoj, C., Maus, S., Olsen, N., Petrov, V., Ridley, V., Rother, M., Sabaka, T. J., Saturnino, D., Schachtschneider, R., Sirol, O., Tangborn, A., Thomson, A., Tøffner-Clausen, L., Vigneron, P., Wardinski, I., and Zvereva, T.: International Geomagnetic Reference Field: the 12th generation, Earth Planets Space, 67, 79, https://doi.org/10.1186/s40623-015-0228-9, 2015. a
Tooley, C. R., Black, R. K., Robertson, B. P., Stone, J. M., Pope, S. E., and Davis, G. T.: The Magnetospheric Multiscale Constellation, Space Sci. Rev., 199, 23–76, https://doi.org/10.1007/s11214-015-0220-5, 2016. a
Torbert, R. B., Russell, C. T., Magnes, W., Ergun, R. E., Lindqvist, P.-A., Le Contel, O., Vaith, H., Macri, J., Myers, S., Rau, D., Needell, J., King, B., Granoff, M., Chutter, M., Dors, I., Olsson, G., Khotyaintsev, Y. V., Eriksson, A., Kletzing, C. A., Bounds, S., Anderson, B., Baumjohann, W., Steller, M., Bromund, K., Le, G., Nakamura, R., Strangeway, R. J., Leinweber, H. K., Tucker, S., Westfall, J., Fischer, D., Plaschke, F., Porter, J., and Lappalainen, K.: The FIELDS Instrument Suite on MMS: Scientific Objectives, Measurements, and Data Products, Space Sci. Rev., 199, 105–135, https://doi.org/10.1007/s11214-014-0109-8, 2016a. a, b
Torbert, R. B., Vaith, H., Granoff, M., Widholm, M., Gaidos, J. A., Briggs, B. H., Dors, I. G., Chutter, M. W., Macri, J., Argall, M., Bodet, D., Needell, J., Steller, M. B., Baumjohann, W., Nakamura, R., Plaschke, F., Ottacher, H., Hasiba, J., Hofmann, K., Kletzing, C. A., Bounds, S. R., Dvorsky, R. T., Sigsbee, K., and Kooi, V.: The Electron Drift Instrument for MMS, Space Sci. Rev., 199, 283–305, https://doi.org/10.1007/s11214-015-0182-7, 2016b. a, b
Torkar, K., Nakamura, R., Tajmar, M., Scharlemann, C., Jeszenszky, H., Laky, G., Fremuth, G., Escoubet, C. P., and Svenes, K.: Active Spacecraft Potential Control Investigation, Space Sci. Rev., 199, 515–544, https://doi.org/10.1007/s11214-014-0049-3, 2016. a
Young, D. T., Burch, J. L., Gomez, R. G., De Los Santos, A., Miller, G. P., Wilson, P., Paschalidis, N., Fuselier, S. A., Pickens, K., Hertzberg, E., Pollock, C. J., Scherrer, J., Wood, P. B., Donald, E. T., Aaron, D., Furman, J., George, D., Gurnee, R. S., Hourani, R. S., Jacques, A., Johnson, T., Orr, T., Pan, K. S., Persyn, S., Pope, S., Roberts, J., Stokes, M. R., Trattner, K. J., and Webster, J. M.: Hot Plasma Composition Analyzer for the Magnetospheric Multiscale Mission, Space Sci. Rev., 199, 407–470, https://doi.org/10.1007/s11214-014-0119-6, 2016. a





